Het twee-spleten-experiment, zoals dat in 1961 uitgevoerd is door de Duitse natuurkundige Clauss Jönsson, is door lezers in een poll in 2002 van het gezaghebbende Physics World uitgeroepen tot het mooiste experiment uit de geschiedenis van de natuurkunde. Zelf sluit ik me daarbij aan. Het experiment bevestigt het bizarre karakter van de quantummechanica. Het is zowel baanbrekend als onvoorstelbaar. Het noopt tot discussies over wat waarnemen (door de mens of een apparaat) eigenlijk is.
Om dit experiment te bespreken moeten we eerst terug naar het jaar 1805, toen Thomas Young met zijn twee-spleten-experiment (in het Engels: double-slit-experiment) aantoonde dat licht uit golven bestaat.

In die tijd was er een heftige discussie tussen Isaac Newton (1643-1727) en onze eigen Christiaan Huygens (1629-1695) of licht nu uit deeltjes bestond of uit golven. Newton wees onder andere op de schaduwwerking van licht, voor hem de bevestiging van een deeltjeskarakter. Huygens wees op het feit van buiging van licht, hetgeen alleen bij golven op kan treden. Ze stonden in hun visie lijnrecht tegenover elkaar. En met hen de hele natuurwetenschap met evenveel aanhangers van Newton als van Huygens.
De proef van Young bestond eruit om een coherente lichtbundel (coherent = licht met dezelfde golflengte en frequentie) op twee spleten te laten schijnen. Achter het scherm stond een scherm opgesteld dat het patroon dat ontstond duidelijk weergaf. Zie hieronder.

                                 De proef van Young (opstelling)

Het bleek dat er op het scherm een interferentiepatroon ontstond, dat wil zeggen dat er plekken ontstonden met veel licht en met weinig licht. Dat kan alleen maar verklaard worden met een golfkarakter. Er treedt namelijk diffractie op. De golven buigen vanaf een spleet bolvormig af, precies als bij watergolven door een nauwe opening, er ontstaat een weglengteverschil vanuit de twee spleten en de golven ontmoeten elkaar op het scherm. Waar twee golfbergen elkaar ontmoeten ontstaat versterking (= constructieve interferentie), dus een scherpe lichtvlek. Waar een golfberg van de ene een golfdal van de andere golf ontmoet ontstaat een uitdoving (= destructieve interferentie), dus een donkere vlek op het scherm. Zie hieronder.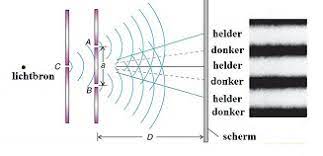


                        De proef van Young (uitgewerkt)

Het golfkarakter van licht was hiermee duidelijk aangetoond. Het pleit leek beslecht, Huygens had gewonnen. Echter, eind 19e eeuw toonde Max Planck aan dat licht uit pakketjes energie bestaat, fotonen genaamd. Planck zelf noemde ze 'kwanta'. Dit was het begin van wat later de quantummechanica werd genoemd.
Albert Einstein ging uit van het deeltjeskarakter van deze fotonen om hiermee het foto-elektrisch effect te kunnen verklaren. Voor deze verklaring kreeg Einstein in 1921 de nobelprijs voor de natuurkunde (en dus niet voor zijn beroemde relativiteitstheorie). 
Het stond nu weer 1 - 1 in de strijd tussen Newton en Huygens. Ze hadden allebei gelijk. Sindsdien spreekt men van de dualiteit van licht: het gedraagt zich soms als een deeltje, soms als een golf. 

Ondertussen had Louis de Broglie in 1923 aangetoond dat deeltjes als elektronen ook een golfkarakter hebben, met andere woorden ze kunnen met elkaar interfereren, dus elkaar versterken of uitdoven. De elektronenmicroscoop is hier onder andere op gebaseerd. 
Een belangrijke relatie werd in 1928 door Werner Heisenberg geformuleerd: je kunt nooit een precieze plek van een deeltje bepalen zonder kennis van de hoeveelheid beweging (= impuls) te verliezen. En andersom, bij een precies bepaalde impuls weet je absoluut niet waar het deeltje zich bevindt. Dit heet de onzekerheidsrelatie van Heisenberg. Deze relatie geeft alleen significante uitkomsten op microscopisch niveau. In onze eigen macroscopische wereld vallen de uitkomsten ruimschoots weg in de meetonnauwkeurigheid die een essentieel onderdeel is van de natuurkunde. Met andere woorden: in de praktijk merken wij er niets van. 

Dan nu het experiment van Jönsson. Hij gebruikte dezelfde opstelling als Thomas Young, maar in plaats van met licht liet hij de twee spleten beschieten met elektronen. Zie hieronder.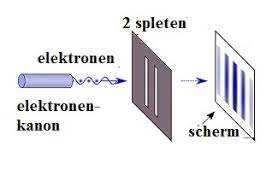


               Twee-spleten-experiment van Jönsson

Zoals verwacht uit het golfkarakter van elektronen ontstaat er op het scherm een interferentiepatroon van lichte en donkere vlekken. Precies zoals bij licht. Maar Jönsson ging verder. Hij vroeg zich af als hij elektronen heel langzaam een voor een op de spleten liet vallen, of er dan ook een interferentiepatroon zou ontstaan. Je zou denken dat een elektron (als deeltje gedacht) door maar één van de twee spleten zou kunnen gaan. Maar dan zou er geen interferentiepatroon optreden. Dat gebeurde wel, zelfs als de elektronen lange tijd na elkaar werden losgelaten, dus was de conclusie dat het elektron door beide spleten tegelijk (!) ging, en daarna met zichzelf interfereerde. Op sommige plekken op het scherm doofde hij zichzelf uit (bij een weglengteverschil van een halve golflengte, anderhalve golflengte etc. vanuit de twee spleten), op andere plekken versterkte hij zichzelf (bij een weglengteverschil van nul, één golflengte etc. vanuit de twee spleten). Bizar natuurlijk, maar een andere conclusie was niet mogelijk. Dit beeld paste ook wel in de onzekerheidsrelatie van Heisenberg, want een deeltje kan geen vaste plek bezitten (door één spleet gaan), zonder zekerheid over de hoeveelheid beweging te verliezen. Het elektron bevond zich dus voor korte tijd op twee plaatsen tegelijk. Of beter gezegd, de kans dat het zich in de ene spleet bevond was even groot als de kans in de tweede spleet. 

Maar het werd nog vreemder. Wanneer men een detector bij een van de spleten plaatste en het elektron als deeltje detecteerde, ontstond er geen interferentiepatroon op het scherm. De waarnemer zorgde kennelijk voor een verstoring van het proces! Het elektron werd gedetecteerd als deeltje en gedroeg zich als deeltje. Hoe is dat te verklaren?
De theorie van de quantummechanica zegt ons dat deeltjes in een continue staat van onzekerheid bestaan. Ze beschikken niet over een specifieke tijd en plaats. Totdat we ze observeren. Ze worden dan als het ware gedwongen om te kiezen. Wij als waarnemer leggen de deeltjes vast door alleen maar waar te nemen. Zo lang we dat niet doen zijn de deeltjes 'vrij', beschikken ze over een golffunctie, en hoeven ze niet te kiezen door welke spleet te gaan. Wij zorgen ervoor dat hun golffunctie instort.

Conclusie: door waar te nemen vernietigen wij alle mogelijkheden op één na. Dat is de werkelijkheid die wij zien. Al het andere is verdwenen, zowel uit ons gezichtsveld als uit de wereld. Resteert de vraag: bestaat er wel een objectieve werkelijkheid? En, als die bestaat, hoe kunnen wij die waarnemen?