Het gebruik maken van zonne-energie is ‘in’ tegenwoordig. Logisch, want de zon levert gratis energie zonder milieuvervuiling. Voor niets gaat de zon op, zou je kunnen zeggen. Pas sinds zo’n 25 jaar maakt men effectief gebruik van de zon als energiebron voor elektriciteit, relatief kort dus.
De theoretische basis voor het opwekken van elektriciteit uit zonne-energie is gelegd door Albert Einstein (1879-1955). Als eerste heeft hij een duidelijke verklaring gegeven voor het optreden van het zogenaamde foto-elektrische effect. Het foto-elektrische effect betekent letterlijk door middel van licht (= foto) een stroom aan elektronen (= elektriciteit) op gang brengen. Dit effect treedt alleen op in metalen.

Metaalrooster met 'vrije' elektronen
Deze beschikken namelijk over een kristalrooster: de atomen zijn dermate regelmatig gerangschikt ten opzichte van elkaar dat de elektronen gemakkelijk van de ene atoomkern naar de andere kunnen overspringen. Het zijn zogenaamde ‘vrije’ elektronen. Het gevolg is dat de elektronen niet sterk aan de kernen van de atomen gebonden zijn en dus makkelijk ‘los’ te maken zijn. Een goede voorwaarde om elektriciteit op te wekken.
Wanneer licht op een metaal valt, is dit dus in staat om elektronen uit het metaal los te maken. Maken we dan een gesloten stroomkring en laten we die elektronen rondgaan, dan hebben we elektriciteit. Zo simpel is het.
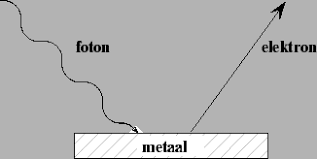
Het foto-elektrisch effect (basaal)
De minimale energie die nodig is om een elektron uit een metaal los te maken noemen we de uittree-energie. Deze is voor elke metaal verschillend. Des te lager de uittree-energie, des te makkelijker worden er elektronen uit het metaal losgeslagen. Eind 19e eeuw had men ontdekt dat licht uit energiepakketjes bestaat, door Max Planck als quanta bestempeld. Later noemde men deze energiepakketjes fotonen. Planck zelf had theoretisch bepaald dat één zo’n energiepakketje een energie heeft van h ꞏ f, waarbij f de frequentie van het licht in Hz is en h de constante van Planck, een zeer klein getal van afgerond 6,626ꞏ10-34 Js.
Dus: Efoton = h ꞏ f
Omdat licht zich met de constante lichtsnelheid c voortplant geldt: c = f ꞏ λ
met λ als de golflengte in m van het licht (makkelijk af te leiden uit v = s /t, met v = c, s = λ, en t = T (= trillingstijd = 1/f).
Hieruit volgt: f = c / λ
Deze twee formules samengevoegd geeft:
Efoton = h ꞏ c / λ
Uit deze formule blijkt dat de energie van een foton alleen afhangt van de golflengte van het licht. Want h en c zijn constanten. Dit is een belangrijke constatering.
Nu bleek uit experimenten dat bij sommige metalen er geen foto-elektrisch effect optrad, ongeacht hoe groot de intensiteit van het opvallende licht was. Dat begreep men niet. Immers, zodra de opvallende energie van het licht meer was dan de uittree-energie van het metaal, zouden er elektronen losgeslagen moeten worden. Grotere intensiteit betekent meer energie. Toch gebeurde dit niet. Men stond voor een raadsel. Toen kwam Einstein met een even simpele als geniale verklaring. Hij beschouwde het foton als een deeltje dat in botsing met het metaal slechts één elektron kon losslaan. Ineens viel alles op zijn plaats. De energie van één foton moet minimaal de uittree-energie van het metaal zijn, dan pas treedt het foto-elektrische effect op. Kennelijk kunnen twee fotonen niet met elkaar samenwerken om de benodigde uittree-energie te laten overstijgen. Achteraf voor de hand liggend, maar ja, kom er maar eens op.
Dus: Efoton ≥ Euittree

Het niet optreden van het foto-elektrisch effect bij rood licht
Wanneer de foton-energie meer is dan de uittree-energie zal het elektron een bepaalde hoeveelheid bewegingsenergie krijgen, ook wel kinetische energie genoemd.
De vergelijking van het foto-elektrisch effect wordt dan:
Efoton = Euittree + Ekin
Maar goed, dan hebben we nog geen elektriciteit. Daartoe hebben we een gesloten stroomkring nodig waar de elektronen doorheen kunnen stromen. Zie de figuur hieronder.
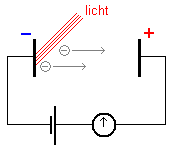
Een gesloten stroomkring
In de stroomkring is een regelbare spanningsbron geplaatst. Die kunnen we zowel positief als negatief maken. Zorgen we ervoor dat de anode (= rechts, waar de elektronen naartoe gaan) positief is, dan zullen de bij het metaal losgemaakte elektronen min of meer worden aangezogen door de anode. Steeds positievere anode betekent steeds meer elektronen die de overkant bereiken, dus een steeds grotere stroom. Tot het moment dat alle elektronen de overkant bereiken, dat is de stroom maximaal, dit noemen we de verzadigingsstroom. Die is dus afhankelijk van het aantal fotonen dat op het metaal valt. Vergroten we het aantal fotonen, dan wordt de verzadigingsstroom hoger. Immers, één foton slaat steeds één elektron los. Zie het plaatje hieronder,

Verzadigingsstroom voorbij punt B
We kunnen de elektronenstroom ook tegenwerken door de anode steeds negatiever te maken. Op een gegeven moment is de anode zo negatief dat zelfs de snelste elektronen de overkant niet meer bereiken. De stroomsterkte is dan 0 ampère. De negatieve spanning waarbij dit optreedt noemen we de remspanning Urem. Zie in de figuur bij punt C.
Alle kinetische energie van de elektronen is opgeheven door de elektrische energie die het gevolg is van het ladingsverschil tussen kathode en anode.
Ofwel:
Ekin = Eel = q ꞏ Urem
Dit geeft voor de formule van het foto-elektrisch effect:
Efoton = Euittree + q ꞏ Urem
waarbij q de lading van het elektron in C (coulomb) is, de elementaire lading e dus.
Veranderen we nu de kleur van het opvallende licht, dan zal de energie van één foton veranderen. De uittree-energie blijft hetzelfde, want deze is alleen afhankelijk van het soort metaal, waardoor de kinetische energie verandert en dus de remspanning Urem.
Blauw licht heeft een kleinere golflengte dan rood licht. Eén foton blauw licht heeft daardoor meer energie dan één foton rood licht (vul maar in de formule in, delen door een kleiner getal levert een grotere uitkomst op).
Met als gevolg dat de remspanning Urem bij blauw licht groter is. Groen zit daar weer tussenin, zowel qua golflengte als remspanning Urem. Zie de figuur hieronder (rood is niet ingetekend maar zou rechts van groen moeten liggen, of levert helemaal geen stroom).

Remspanningen bij blauw en groen licht
In de praktijk zal voor veel metalen rood licht geen elektriciteit opleveren. Eén foton rood licht levert dan niet genoeg energie om één elektron los te slaan. Dit kun je met de zogenaamde grensgolflengte voor metalen zelf uitzoeken. In tabel 24 van BiNaS, het informatieboek voor natuurwetenschappen, een toegestaan middel voor de examens biologie, scheikunde en natuurkunde, staan ze overzichtelijk onder elkaar. Samen met tabel 19A, het elektromagnetisch spectrum van zichtbaar licht, zie je bijvoorbeeld dat rood licht alleen bij cesium een foto-elektrisch effect laat optreden. In de praktijk hebben we zodoende aan het rode licht van de zon bar weinig. Des te meer aan het blauwe licht en het ultraviolette gedeelte van de zon.
Albert Einstein zou voor deze verklaring van het foto-elektrisch effect in 1921 de Nobelprijs voor natuurkunde krijgen. In het wonderjaar 1905 geschreven en gepubliceerd, evenals zijn geniale verklaring van de Brownse beweging en zijn speciale relativiteitstheorie. Pas later, met zijn verbluffende Algemene Relativiteitstheorie in 1915, zou hij wereldberoemd worden.
Op YouTube staan vaak verhelderende filmpjes met uitleg over verschillende natuurkunde onderwerpen. Wat mij betreft springen die van Jeroen Bruijstens er in positieve zin bovenuit. Zie bijvoorbeeld hier zijn uitleg van de fotocel, inclusief commentaar(!).

