De streepjescode, ofwel barcode, kennen we allemaal. Al in 1952 is deze ontwikkeld. Sinds de jaren 70 wordt de streepjescode overal gebruikt om in winkels bij de kassa producten te scannen. Vergelijkbaar hiermee is de ISBN, de code die aan iedere boekuitgave wordt toegekend. Minder bekend is de wiskunde die in zo’n code besloten ligt.
Elk streepje in de code staat voor een cijfer tussen 0 en 9. De scanner leest met behulp van een infrarode lichtbundel de streepjes en vertaalt deze in de bijhorende cijfers. De eerste en de laatste drie streepjes zijn start- en stopcodes. Tussen start en stop zit de code verborgen. De zwarte strepen zijn enen, de witte strepen nullen. In het rijtje cijfers waarmee de code correspondeert zit informatie over het product verborgen, waardoor de computer weet welk product er verkocht is.
Een streepjescode bestaat uit 13 cijfers. De eerste 12 cijfers geven aan wie de fabrikant is en welk product het is. Het laatste cijfer zorgt ervoor dat de streepjescode geldig is. Met andere woorden, het is een soort van controlecijfer (een check digit).
Want, de streepjescode is niet willekeurig. Ze moet aan een aantal voorwaarden voldoen.
1. Tel op: de cijfers op de oneven posities (1,3, etc.), plus de cijfers op de even posities (2,4, etc.), deze laatste vermenigvuldigd met 3.
2. De som van het totaal moet dan deelbaar zijn door 10.
Voorbeeld:
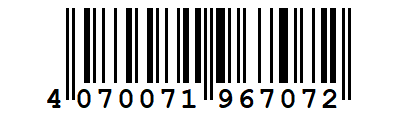
Tellen we op, eerst oneven: 4 + 7 + 0 + 1 + 6 + 0 + 2 = 20
Daarna, de even cijfers x 3: 3 x (0 + 0 + 7 + 9 + 7 + 7) = 3 x 30 = 90
Totaal geeft dat: 20 + 90 = 110 is deelbaar door 10.
Bovenstaand streepjescode is een voorbeeld van EAN (= European Article Number). Wanneer bij het inscannen een fout optreedt, doordat bijvoorbeeld één streepje in een verkeerd cijfer wordt omgezet, dan herkent de computer dit meteen. Het totaal, zoals hierboven berekend, is dan niet deelbaar door 10. De caissière ziet dat het scannen niet is gelukt en kan het opnieuw proberen, of de code met de hand intypen.
Echter, wanneer bij het met de hand intypen twee cijfers worden verwisseld, kan er alsnog iets misgaan. Dat geldt voor de gevallen het even getal 3 wordt verwisseld met het naastgelegen oneven getal 9, of 6 met 2, of 3 met 1. Ga maar na, 3x3 + 9x1 = 18 en 9x1 + 3x3 = 18. Deze fout zal dus niet herkend worden. Er wordt dan een ander product aangeslagen en in rekening gebracht. Feilloos is deze methode dus niet.
De ISBN code bij boeken werkte aanvankelijk met 10 cijfers. De eerste negen cijfers gaven informatie over het boek (land, uitgever, soort literatuur), de laatste zorgde voor de foutherkenning. Hierbij gold als wiskundige regel:
Neem 10 maal het eerste cijfer, 9 maal het tweede, 8 maal het derde, tot uiteindelijk 1 maal het laatste cijfer. Tel dit alles bij elkaar op. De optelsom moet dan deelbaar zijn door 11.
Bijvoorbeeld de ISBN code van mijn eigen boek (Van herfst tot zomer, uitgeverij Christofoor, 2000): 90-6238-681-4. Zie de bovenste regel.

Uitleg van de code: het getal 90 staat voor Nederland, het getal 6238 voor de uitgever (in dit geval Christofoor), het getal 681 voor de uitgave, getal 4 is het controlegetal.
Dit geeft: 10x9 + 9x0 + 8x6 + 7x2 + 6x3 + 5x8 + 4x6 + 3x8 + 2x1 + 1x4 = 264
Het getal 264 is deelbaar door 11 (264/11 = 24).
Zodra een streepje verkeerd vertaald wordt, zal de computer dit als fout herkennen. Er zijn ook geen verwisselingen mogelijk als bij de 13-cijferige streepjescode. Een veilig systeem dus.
Echter, niet elk 9-cijferig rijtje is met één cijfer aan te vullen tot een geldige ISBN code. Wanneer x = y x 11 + 1 is, gaat het mis. Reken maar na. Stel dat x = 111. Met geen mogelijkheid is dan middels een getal van 0 t/m 9 het eerstvolgende getal deelbaar door 11 (hier 121) te bereiken.
Dit probleem heeft men opgelost door op de laatste plaats in de ISBN code het symbool X toe te laten. Deze Romeinse letter X lezen we als 10. Het staat wat raar, maar zo wist men problemen te omzeilen.
Sinds 1 januari 2007 gebruikt men in plaats van deze ISBN-10 codering nu ook de code die hetzelfde werkt als EAN. Het heet nu ISBN-13. Met dezelfde regels als bij EAN. Het is de oude code, aangevuld met de begincijfers 978. Zie de onderste regel. Of, zoals bij mijn boek Jaarfeesten; achtergronden en betekenis in onze tijd, uitgeverij Christofoor, 2017. Zie hieronder.

Passen we weer de regels van de 13-cijferige code toe, dan is:
1. 9 + 8 + 0 + 0 + 8 + 2 + 7 = 34
2. 3 x (7 + 9 + 6 + 3 + 8 + 9) = 3 x 42 = 126
Opgeteld levert dat 34 + 126 = 160. Inderdaad, deelbaar door 10.
Een nadeel is, zoals eerder aangegeven, dat ISBN-13 minder fouten herkent dan ISBN-10.

