Aan het begin van de 20e eeuw was kwam men erachter dat de natuur in hoge mate gekwantiseerd is. Waarmee bedoeld wordt: er is van een grootheid een kleinste vorm aanwezig is dat niet meer deelbaar is. Zo had men eerder geconstateerd dat materie uit atomen bestaat. Atoom betekent letterlijk ondeelbaar. Een atoom kun je niet in tweeën hakken. Alle materie blijkt opgebouwd te zijn uit (een grote hoeveelheid) atomen. Zo is ook licht gekwantiseerd. Het bestaat uit kleine energiepakketjes, fotonen genoemd. Ook een foton kun je niet in tweeën delen.
Zo ontstond ook het vermoeden dat lading gekwantiseerd is. Tussen 1909 en 1913 heeft Robert Millikan samen met Harvey Fletcher een experiment bedacht om dit enerzijds aan te tonen en anderzijds de kleinst mogelijke lading, ook wel de elementaire lading genoemd, nauwkeurig te bepalen. Het is een van de beroemdste experimenten uit de natuurkunde, waarvoor Millikan in 1923 dan ook de Nobelprijs kreeg.
De proef ziet er eenvoudig uit. Millikan liet oliedruppeltjes tussen twee condensatorplaten vallen. Met behulp van röntgenstraling zorgde hij ervoor dat in de lucht tussen de platen elektronen vrijkwamen. Deze hechtten zich vervolgens aan de oliedruppels, die daardoor negatief geladen werden. Door de spanning tussen de condensatorplaten (bovenste plaat positief, onderste plaat negatief) te variëren kon hij sommige druppeltjes stil laten staan. Want de bovenste positieve plaat trekt de negatief geladen druppels naar zich toe, tegen de zwaartekrracht in. Zie de schets hieronder.
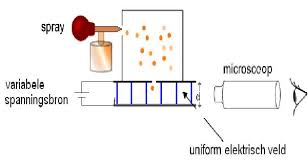
De proef van MIllikan
Er werken nu drie krachten op de oliedruppeltjes: de zwaartekracht naar beneden, de elektrische kracht en de opwaartse kracht (de weerstand van de lucht) naar boven. Deze zijn in evenwicht, dus volgens de eerste wet van Newton is de resulterende kracht gelijk aan 0 N.
Fres = Fnaar boven – Fnaar beneden = 0
Ofwel Fel + Fopw = Fz
De volgende formules gelden:
Fel = q ꞏ U waarbij q de lading is in C en U de spanning in V.
Fopw = ρluchtꞏVꞏg waarbij ρlucht de dichtheid van lucht is in kg/m3, V het volume van een
druppeltje in m3 en g de valversnelling op aarde (= 9,81 m/s2).
Fz = mꞏg waarbij m de massa van een druppeltje is in kg en g weer de valversnelling in m/s2.
Tegelijk geldt dat m = ρolieꞏV met ρolie als de dichtheid van olie in kg/m3 en V weer het volume
van een oliedruppeltje in m3.
Verder geldt voor een bolvormig druppeltje: V = 4/3 πꞏr3 waarbij r de straal van een druppeltje is in m. Deze straal kon hij door nauwkeurig door een microscoop naar zo’n zwevend druppeltje te kijken redelijk nauwkeurig bepalen.
De totale formule voor de lading van een druppeltje wordt zodoende:
q ꞏ U + ρluchtꞏVꞏg = ρolieꞏVꞏg --> q ꞏ U = ρolieꞏVꞏg - ρluchtꞏVꞏg = ( ρolie - ρlucht) ꞏVꞏg
Ofwel q = ( ρolie - ρlucht) ꞏ4πꞏr3ꞏg / 3U
Zowel ρolie als ρlucht zijn bekend, evenals g. De straal r werd middels de microscoop opgemeten, de spanning U werd zo ingesteld dat het geobserveerde druppeltje precies bleef zweven.
Millikan kreeg steeds een andere uitkomst bij zijn berekeningen van de lading q van de verschillende druppeltjes. Wat logisch was, want het ene druppeltje was groter en dus zwaarder dan het andere. Met dus ook meer of minder (negatieve) lading.
Maar, na meting van duizenden druppeltjes kwam hij tot de conclusie dat al die verschillende ladingen deelbaar waren door steeds eenzelfde getal. Dat getal moest dan wel de kleinst denkbare lading zijn! Deze lading heette vanaf dat moment de elementaire lading e. Deze blijkt 1,602ꞏ10-19 C te zijn.
Het experiment ziet er eenvoudig uit. In de praktijk blijkt het echter ontzettend moeilijk om bepaalde druppeltjes exact zwevend te houden. Ze vliegen al heel gauw naar boven en naar onderen. Tot frustratie van al die studenten natuurkunde die dit experiment wel even na zouden doen. Heel bijzonder dat Millikan dan tot zulke exacte resultaten kwam.
Het blijkt dan ook dat Millikan enigszins met zijn resultaten heeft geknoeid. Hij kwam, beweerde hij, bij zijn bepaling van e uit op een nauwkeurigheid van 0,5 %, wat achteraf (bleek na naberekeningen) in feite 2 % had moeten zijn. Metingen die te veel buiten het gemiddelde vielen heeft hij namelijk weggelaten. Niet echt fraai natuurlijk, maar zo gaat dat er in de praktijk soms aan toe. Dat neemt niet weg dat zijn onderzoek alsmede het resultaat toentertijd baanbrekend was. Die elementaire lading van 1,602ꞏ10-19 C staat nog altijd als een huis. Tot in lengte van dagen (en jaren, en eeuwen, en... ).

