Het verschijnsel licht heeft in de natuurkunde altijd voor verwarring en controverses gezorgd. Onze eigen Christiaan Huijgens meende dat licht uit golven bestond, hetgeen hij kon aantonen met buigings- en interferentieverschijnselen. Isaac Newton, de grondlegger van de hedendaagse natuurkunde, beweerde dat licht uit deeltjes bestond. Hij wees er onder andere op dat licht altijd rechtdoor gaat (waardoor er bijvoorbeeld schaduwwerking optreedt).
Begin 20e eeuw kwam men tot de conclusie dat beiden min of meer gelijk hadden. Licht gedraagt zich soms als een deeltje en soms als een golf. Dit heet: licht heeft een dualistisch karakter. Nauwkeuriger geformuleerd: licht bestaat uit energiepakketjes, fotonen genaamd, die zich als golven kunnen gedragen. Wanneer gedragen ze zich als golven? Antwoord, wanneer wij ze als golven detecteren (= waarnemen). Wanneer gedragen ze zich als deeltjes? Antwoord: wanneer wij ze als deeltjes detecteren. Zie het bekende double slit experiment, ook wel de proef van Young genoemd.
Opzienbarend, dat de waarnemer bepaalt wat er gebeurt. Ofwel, zoals dat in de quantummechanica wordt genoemd, zoals de waarnemer de gebeurtenis verstoort.
Andersom, elk bewegend deeltje, zoals bijvoorbeeld een elektron, heeft ook golfeigenschappen. Tot deze ontdekking kwam De Broglie in 1924. De golflengte van zo'n deeltje wordt dan ook een De Broglie-golflengte genoemd. Deze is een constante (die van Planck) gedeeld door de impuls van het deeltje.
Hiervan wordt gebruik gemaakt bij de elektronenmicroscoop, die zo'n 1000 keer nauwkeuriger kan waarnemen dan de gewone lichtmicroscoop (die zijn begrenzing vindt in het feit dat zichtbare lichtdeeltjes - fotonen - tussen de 380 en 780 nm groot zijn, dus tussen de 0,00038 en 0,00078 mm: wanneer het te bestuderen object kleiner is dan dit formaat, buigen de fotonen er omheen en worden ze dus niet weerkaatst).
Maar, een veel belangrijker gevolg van het feit dat elektronen een golfkarakter hebben, is de verklaring van de elektronenbanen om de kern in een atoom.
Rutherford had in 1911 ontdekt dat elektronen in banen rond een kern van protonen en neutronen circuleerden. Maar dit idee was zeer onvolledig, omdat niets de elektronen ervan zou weerhouden zich op de kern te storten. Niels Bohr postuleerde in 1913 dat de elektronen zich alleen in bepaalde stationaire banen konden bevinden. Waarom dat zo was kon hij niet verklaren. Stralingsenergie kwam alleen vrij wanneer een elektron van de ene stabiele baan naar een andere (meer naar binnen gelegen) baan oversprong.
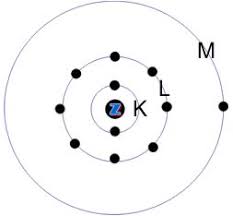
Atoommodel van Bohr
Pas door de ontdekking van het golfkarakter van elektronen, kon men (ook wiskundig) de stationaire banen verklaren. En ook, waarom er in de binnenste schil (de K-schil) maximaal maar twee elektronen kunnen voorkomen, in de volgende schil (de L-schil) maximaal acht elektronen etc.
In de omloop om de kern heen passen in de K-schil precies één of twee golflengten! Niet meer, daarvoor is de afstand te kort. Dat wil zeggen, wanneer de omtrek van de denkbeeldige cirkel (in werkelijkheid is het een ellips) de juiste afmeting heeft, bij de K-schil één of twee golflengten, dan is er een stabiele toestand. De golven interfereren met elkaar, houden elkaar in stand, precies als bij een staande golf in een snaar van een gitaar.
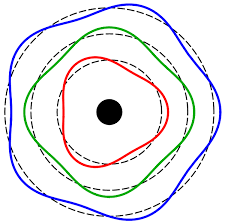
Elektronengolven die met elkaar interfereren
en elkaar dus in stand houden
Die analogie met de staande golf bij een gitaar is uiterst belangrijk om het begrip nulpuntsenergie te begrijpen. Een deeltje opgesloten in een kleine oneindig diepe put golft als het ware steeds heen en weer tussen de wanden van de put. Vergelijkbaar met de trilling in een snaar, waar een lopende golf met grote snelheid (zo'n 500 m/s) van links naar rechts en weer terug tussen de uiteinden (de knopen) beweegt. De toon die we horen is de grondtoon.
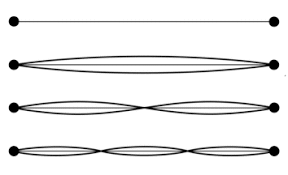
Grondtoon en boventonen in een snaar (Helemaal boven: stilstaande snaar. Daaronder: grondtoon.
Daar weer onder: 1e boventoon. Onderste tekening: 2e boventoon)
Maar tegelijk trilt de snaar in de eerste boventoon, in de tweede boventoon etc. Deze tonen horen we bovenop de grondtoon, tegelijkertijd. Deze zorgen voor het zuiver klinken van de toon. Is de snaar niet goed gestemd, dan passen de boventonen niet goed in de grondtoon en ervaren we het geluid als vals.
Kenmerk: de lengte van de snaar is steeds n keer een halve golflengte (waarbij n = 1,2,3 etc.). Voor de grondtoon geldt: n=1. Voor de 1e boventoon: n=2 etc.
Zo gebeurt dat ook met een deeltje in een kleine ruimte met oneindig hoge wanden. Ook hier is een grondtoestand aanwezig. Het deeltje heeft energiewaarden overeenkomstig de verschillende trillingen van een snaar. Wiskundig is af te leiden, vanuit de zogenaamde Schrödingervergelijking, dat het deeltje een golfgetal k heeft dat gelijk is aan 2π gedeeld door de golflengte. De energiewaarden van het deeltje zijn dus gekwantiseerd. Maar, let wel, dit geldt alleen voor deeltjes in een kleine ruimte. Wanneer een deeltje volledig vrij is, dus wanneer het niet is opgesloten, kan de energie elke willekeurige positieve waarde hebben.
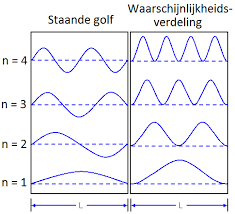
Deeltje in put, toestandsfunctie Deeltje in put, waarschijnlijkheidsverdeling
Evenwel, wiskundig kan afgeleid worden dat de grondtoestand van een deeltje een constante is gedeeld door de massa en het kwadraat van de bewegingsruimte. Deze is dus ongelijk aan nul. Zelfs bij het absolute nulpunt (0 K = -273,16 °C) heeft een deeltje dus nog energie. Dit wordt de nulpuntsenergie genoemd.
Deze nulpuntsenergie is te begrijpen uit de beroemde onzekerheidsrelatie van Heisenberg. Weet je nauwkeurig de plaats van een deeltje, dan is zijn impuls in grote mate onbekend, en andersom, weet je nauwkeurig de impuls van een deeltje, dan is zijn plaats in grote mate onbekend (met als verhouding de constante van Planck).
Is de ruimte klein, zoals in een diepe put, dan weet je vrij nauwkeurig de plaats en dan moet er in de grondtoestand een bepaalde impuls zijn, en dus een bepaalde energie.
Je kunt uitrekenen hoeveel die energie is voor een bepaalde massa. Neem een massa van 0,1 kg dat kan bewegen in een buis van 1 meter lengte. De nulpuntsenergie (uitgedrukt in joule) is dan een getal van 68 nullen achter de komma. Interessanter misschien: het voorwerp ligt niet echt stil, maar beweegt met een snelheid van een getal van 33 nullen achter de komma (meter per seconde) heen en weer. Het zal in 1023 jaar van de ene kant van de buis naar de andere zijn bewogen! Dit gaat zo langzaam dat wij gewoonlijk zeggen: het voorwerp ligt stil.
De nulpuntsenergie is de laagst mogelijke energiewaarde die een deeltje (en dus ook een massa) kan hebben. Lager kan niet. Tot werkelijk nul kun je dus niet komen. Dat betekent dat je er, hoewel sommigen anders beweren, in de praktijk niets mee kunt. Je kunt deze energie niet aftappen of op een bepaalde manier "vrij maken". Dit is in strijd met de onzekerheidsrelatie van Heisenberg, zoals gememoreerd, maar ook met de tweede hoofdwet van de thermodynamica die zegt dat energie alleen van een hogere naar een lagere toestand kan stromen. Andersom, van een lagere toestand naar een hogere kan niet.
Toch heeft het bestaan van de nulpuntsenergie in de kosmologie interessante ontdekkingen teweeg gebracht. Met name het Casimir-effect, het optreden van kwantumeffecten in een vacuümruimte, is bijzonder. Deeltjes en hun antideeltjes kunnen zo voor heel even uit "het niets" ontstaan, om elkaar dan ogenblikkelijk weer uit te doven. Kortom, een absoluut vacuüm bestaat niet. Het niets bestaat quantummechanisch gezien uit een steeds weer onverwachts en heel kortstondig optredend iets en een anti-iets. Fascinerend.


Nog een kleine correctie/aanvulling overigens: de thermodynamica verbiedt niet dat energie van een lagere naar een hogere toestand kan stromen, want in feite doet een koelkast dat. De thermodynamica zegt er bij, dat dat niet kan zonder dat er arbeid wordt verricht. Anders gezegd: spontaan en zonder invloed/aktie van buiten stroomt energie inderdaad altijd van een hogere naar een lagere toestand.
Over die nulpuntsenergie: veel complotdenkers grijpen dit begrip aan om aan te tonen dat de NWO (De Nieuwe Wereldorde) ons informatie achterhoudt. Omdat de nulpuntsenergie niet nul is, zou er gratis energie beschikbaar zijn. Echter, omgekochte wetenschappers, in dienst van de NWO, houden dit tegen. Niemand die dit weet, het is geheime informatie. Alleen wakkere complotdenkers prikken hier doorheen.
Zo heb ikzelf een keer op mijn tante gereageerd die heilig in dit soort komplottheorieën gelooft. Met argumenten zoals in mijn artikel geformuleerd. Hoewel zij qua onderwijs niet meer dan de huishoudschool heeft genoten, beweerde ze nogal smalend dat ik er kennelijk niet zo veel verstand van had. Zij wel. Discussie gesloten.